【문제】
계단 수(n)와 한번에 오를 수 있는 최대 수(m)가 주어 졌을 때, 계단을 오를 수 있는 경우의 수를 구하시오.
(단, 0 < n < 100, 0 < m < n)
【예시】
- 계단 수 (n) : 3, 한번에 오를 수 있는 최대 수(m) : 3
- 최대 1칸 뛰어넘을 때 : ㅁ + ㅁ + ㅁ -> 1개
- 최대 2칸 뛰어넘을 때 : ㅁ + ㅁㅁ, ㅁㅁ + ㅁ -> 2개
- 최대 3칸 뛰어넘을 때 : ㅁㅁㅁ -> 1개
경우의 수 : 4
【입출력 예시】
| 【입력 예시 1】 | 【출력 예시 1】 | 【입력 예시 2】 | 【출력 예시 2】 |
|---|---|---|---|
| 5 5 | 16 | 6 3 | 24 |
【문제 풀이】
이 문제를 풀기 위해선 알아야 할 사실이 있다.
먼저 어떤 사람이 계단을 올라갈 때 0개의 계단을 오르는 방법과 1개의 계단을 오르는 방법은 모두 1개이다. 왜냐하면 0개는 안움직이면 되는 것이고 1개의 계단은 그냥 1개를 올라가면 되는 것이기 때문이다.
f(n,m)을 한번에 m보다 작은 자연수의 계단을 올라갈 수 있는 사람이 n개의 계단을 올라가는 방법의 수를 구하는 함수라고 했을 때 어떤 사람이 0개의 계단과 1개의 계단을 올라가는 방법의 수는 각각 1개이다.(단, n과 m은 자연수)
이를 식으로 표현하면 f(0,m) == f(1,m) == 1(m은 0보다 큰 자연수)이 된다. 이 사실을 염두해 두고 풀이를 진행하겠다.
그렇다면 f(2,2)는 어떨까?

위 그림을 보면 2개의 계단이 있고 빨간색 사람은 1층에 초록색 사람은 0층이 서있다. 여기서 빨간색 사람은 2층까지 1계단만 올라가면 모든 계단을 등반하는 것이고 초록색 사람은 2개의 계단을 오르면 모든 계단을 등반하는 것이다.
그렇다면 이 두 사람이 서있는 위치에서의 f(n,m)은 어떻게 될까?
만약 올라야하는 계단의 수가 1이라면 빨간색 사람이 서있는 위치가 최종 도착점이 될 것이고 올라야하는 계단의 수가 0이라면 초록색 사람이 서있는 위치가 최종 도착점이 될 것이다.
그런데 빨간색 사람과 초록색 사람은 이미 1층과 0층이 각각 서있다. 즉, 최종 도착점이 1층일 때와 0층일 때 빨간색 사람과 초록색 사람은 이미 최종 도착점에 도달한 것이다.
즉 두 사람이 서있는 위치에서의 f(n,m)은 빨간색 사람은 f(1,m), 초록색 사람은 f(0,m)이 된 것이다. (최종 목표인 n이 각각 1과 0이기 때문에)
정리하자면 두 사람이 있는 위치에서 1칸 혹은 2칸만 올라가면 2칸의 계단을 모두 등반한것이 되니 두 사람의 위치까지 올라가는 경우의 수를 더하면 f(2,2)가 나오는데 두 사람의 위치까지 올라가는 경우의 수는 각각 f(1,m)과 f(0,m)이고 이는 우리가 제일 처음에 확인했듯이 1이기 때문에 f(2,2) = f(0,2) + f(1,2) = 1 + 1 = 2가 된다. 따라서 f(2,2)는 2가 된다.
여기서 우리가 중요시 해야하는 개념은 바로 1칸 혹은 2칸 올라가면 최종 목적지에 올라갈 수 있는 위치까지 올라갈 수 있는 경우의 수를 모두 더하면 우리가 최종적으로 올라가고자 하는 위치까지 가는 경우의 수를 알 수 있다는 점이다.
이 개념만 알고 있다면 n과 m이 몇이 오든간에 f(n,m)을 서브 항목으로 나눌 수 있다.
예를 들어서 그렇다면 f(3,3)은 값이 뭘까?

f(3,3)은 위 그림과 같이 세 사람이 서있는 위치로 표현할 수 있다.
이를 식으로 표현하면 다음과 같다.
f(3,3) = f(0,3) + f(1,3) + f(2,3)
이 식들 보면 또 한가지 의문점이 들 수 있는데 만약 m이 n보다 크다면 그것은 무엇을 의미하는 것일까?
f(2,3)은 2개의 계단을 올라가지만 한 번에 3개의 계단을 올라갈 수 있는 경우의 수이다. 하지만 2개까지만 올라가면 되니 3개의 계단을 올라가는 경우의 수는 카운트하지 않는다. 따라서 f(2,3) == f(2,2)와 같다. f(0,3)과 f(1,3) 도 f(0,0)과 f(1,1)과 같다.
그리고 이는 우리가 전에 구했던 값들로 알 수 있다.
f(0,3)과 f(1,3)은 1, f(2,3)은 2이다.
따라서 f(3,3) = f(0,3) + f(1,3) + f(2,3) = 1 + 1 + 2 = 4가 된다.
마지막으로 다른 예를 한 번 들어보자
이번엔 n≠m인 경우를 살펴보자.
f(3,2)는 한 번에 2개의 계단을 올라갈 수 있는 사람이 최종적으로 3층 계단까지 도달하는 경우의 수이다.
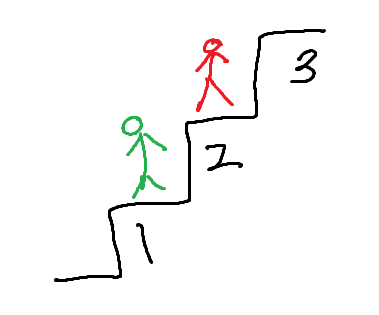
이는 위 그림과 같이 표현할 수 있다. 빨간색 사람은 1칸만 올라가면, 초록색 사람은 2칸만 올라가면 최종 계단에 오를 수 있는 상태이다. 이 상태를 식으로 나타내면
f(3,2) = f(2,2) + f(1,2)가 된다. 즉, f(3,3)에서 f(0,3)이 빠진 값이 되며 이는 f(3,2)가 f(3,3)보다 1이 작다는 것을 유추할 수 있다.
위와 같은 정보들을 통하여 우리는 점화식을 유추해볼 수 있다.
f(n,m) = f(n-1,m) + f(n-2,m) + ... f(n-m,m)
그렇다면 우리가 필요한 정보는 모두 얻었으니 코드를 작성해보자.
코드는 매우 단순하다.

먼저 "n m"을 입력받아서 저장하고 계단함수에 인자를 전달한다.

인자를 받으면 계단 함수는 n이 1보다 작거나 같은지 검사하여 참이라면 1이라는 값을 리턴해준다.

n이 1이 아니라면 for문을 반복하면서 way라는 변수에 f(n-1,m), f(n-2,m), f(n-3,m) ... f(n-m,m)을 차례로 더해준 뒤 way를 리턴한다.
for문을 도는 도중 만약 i가 n보다 커진다면 n-i를 할 시 음수값이 반환되기 때문에 이러한 경우는 카운팅에서 제외시켜주기 위하여 break문을 써서 탈출하도록 하였다.
이게 끝이다.
【전체코드】
|
1
2
3
4
5
6
7
8
9
10
11
12
|
def stair(n,m):
if n <= 1: return 1
else:
way = 0
for i in range(1,m+1):
if i > n: break
way += stair(n-i,m)
return way
if __name__=='__main__':
n,m = map(int,input().split())
print(stair(n,m))
|
cs |
【느낀점】
처음에 이 문제를 풀기 위해서 직접 경우를 세는 방향으로 코딩을 했었다.
그랬는데 완전 뻘짓이었다. 이 문제의 핵심은 실제로 올라가는 방법을 구한다음 갯수를 세는 것이 아닌 재귀를 통하여 결과값을 더하여 해결하는 것이다.
그렇다면 만약 등반하는 모든 경우를 출력하라고 한다면 어떻게 해야할까?
또한 재귀를 통해 풀 수 있는 문제는 동적 프로그래밍을 통해서도 해결할 수 있는데 동적 프로그래밍을 코딩을 한다면 어떻게 짜야할까?
궁금하다.